# Instalación y carga de paquetes necesarios
## Para manipulación y visualización de datos
if (!require(tidyverse)) install.packages("tidyverse")
## Para exportar archivos en excel
if (!require(writexl)) install.packages("writexl")
## Para importar archivos en excel
if (!require(readxl)) install.packages("readxl")12 Ejemplo en R
12.1 Base de datos
Referencia del dataset: Fisher, R. (1936). Iris [Dataset]. UCI Machine Learning Repository. https://doi.org/10.24432/C56C76
Acceso a recursos: El script completo con el ejemplo desarrollado y la base de datos IRIS pueden descargarse en el siguiente repositorio: https://github.com/Ludwing-MJ/MTCDPR_datos_agrupados
A continuación, se presenta un conjunto de datos correspondientes a la longitud del pétalo (en cm) de 150 flores de la especie Iris, organizados en formato matricial para facilitar su visualización y análisis. Estos datos serán utilizados para ilustrar el cálculo de estadísticos descriptivos para datos agrupados, siguiendo las metodologías propuestas en la sección anterior.
| 1.4 | 1.4 | 1.3 | 1.5 | 1.4 | 1.7 | 1.4 | 1.5 | 1.4 | 1.5 |
| 1.5 | 1.6 | 1.4 | 1.1 | 1.2 | 1.5 | 1.3 | 1.4 | 1.7 | 1.5 |
| 1.7 | 1.5 | 1.0 | 1.7 | 1.9 | 1.6 | 1.6 | 1.5 | 1.4 | 1.6 |
| 1.6 | 1.5 | 1.5 | 1.4 | 1.5 | 1.2 | 1.3 | 1.4 | 1.3 | 1.5 |
| 1.3 | 1.3 | 1.3 | 1.6 | 1.9 | 1.4 | 1.6 | 1.4 | 1.5 | 1.4 |
| 4.7 | 4.5 | 4.9 | 4.0 | 4.6 | 4.5 | 4.7 | 3.3 | 4.6 | 3.9 |
| 3.5 | 4.2 | 4.0 | 4.7 | 3.6 | 4.4 | 4.5 | 4.1 | 4.5 | 3.9 |
| 4.8 | 4.0 | 4.9 | 4.7 | 4.3 | 4.4 | 4.8 | 5.0 | 4.5 | 3.5 |
| 3.8 | 3.7 | 3.9 | 5.1 | 4.5 | 4.5 | 4.7 | 4.4 | 4.1 | 4.0 |
| 4.4 | 4.6 | 4.0 | 3.3 | 4.2 | 4.2 | 4.2 | 4.3 | 3.0 | 4.1 |
| 6.0 | 5.1 | 5.9 | 5.6 | 5.8 | 6.6 | 4.5 | 6.3 | 5.8 | 6.1 |
| 5.1 | 5.3 | 5.5 | 5.0 | 5.1 | 5.3 | 5.5 | 6.7 | 6.9 | 5.0 |
| 5.7 | 4.9 | 6.7 | 4.9 | 5.7 | 6.0 | 4.8 | 4.9 | 5.6 | 5.8 |
| 6.1 | 6.4 | 5.6 | 5.1 | 5.6 | 6.1 | 5.6 | 5.5 | 4.8 | 5.4 |
| 5.6 | 5.1 | 5.1 | 5.9 | 5.7 | 5.2 | 5.0 | 5.2 | 5.4 | 5.1 |
12.2 Preparación del entorno de trabajo
12.3 Carga y Preparación de Datos
Primero, se carga el conjunto de datos iris y se extrae la variable de interés, en este caso, la longitud del pétalo.
# Cargar el dataset iris
data(iris)
# Extraer la variable longitud de pétalo
longitud_petalo <- iris$Petal.Length12.4 Determinación de parámetros básicos para la agrupación
Se define una función personalizada para calcular los parámetros necesarios para agrupar los datos: número de observaciones, valores mínimo y máximo, rango, número de clases (usando la regla de Sturges) y amplitud de clase.
# Función para calcular parámetros de agrupamiento
calcular_parametros_agrupamiento <- function(datos) {
n <- length(datos)
x_min <- min(datos)
x_max <- max(datos)
rango <- x_max - x_min
# Regla de Sturges para número de clases
k <- round(1 + 3.322 * log10(n))
# Amplitud de clase
amplitud <- rango / k
return(list(
n = n,
x_min = x_min,
x_max = x_max,
rango = rango,
k = k,
amplitud = amplitud
))
}Una vez ya definida la función para calcular los parámetros necesarios para la agrupación de los datos (tarea que se realiza la cada vez que se abre el software y se desea cargar la función en el entorno de trabajo). Se procede a calcularlos:
# Aplicar función
parametros <- calcular_parametros_agrupamiento(longitud_petalo)
# Visualizar el resultado
parametros$n
[1] 150
$x_min
[1] 1
$x_max
[1] 6.9
$rango
[1] 5.9
$k
[1] 8
$amplitud
[1] 0.737512.5 Construcción de la tabla de frecuencias
Se utiliza una función personalizada para construir la tabla de frecuencias, calculando los límites de clase, marcas de clase, frecuencias absolutas, relativas y acumuladas, así como sumas necesarias para los cálculos posteriores.
# Función corregida para construir tabla de frecuencias
construir_tabla_frecuencias <- function(datos, parametros) {
# Crear breaks (puntos de corte) para las clases
# Esto garantiza exactamente k clases
breaks <- seq(parametros$x_min,
parametros$x_max,
length.out = parametros$k + 1)
# Crear límites de clase a partir de los breaks
limite_inferior <- breaks[-length(breaks)] # Todos excepto el último
limite_superior <- breaks[-1] # Todos excepto el primero
# Calcular marcas de clase
marca_clase <- (limite_inferior + limite_superior) / 2
# Calcular frecuencias absolutas usando cut()
intervalos <- cut(datos,
breaks = breaks,
include.lowest = TRUE,
right = FALSE,
labels = FALSE) # Usar números en lugar de etiquetas
# Contar frecuencias por clase
frecuencia_absoluta <- as.numeric(table(factor(intervalos,
levels = 1:parametros$k)))
# Reemplazar NA por 0 si alguna clase queda vacía
frecuencia_absoluta[is.na(frecuencia_absoluta)] <- 0
# Calcular frecuencias derivadas
frecuencia_relativa <- frecuencia_absoluta / parametros$n
frecuencia_acumulada <- cumsum(frecuencia_absoluta)
fi_xi <- frecuencia_absoluta * marca_clase
fi_xi2 <- frecuencia_absoluta * (marca_clase^2)
# Crear tabla
tabla <- data.frame(
Clase = 1:parametros$k,
Limite_Inferior = round(limite_inferior, 3),
Limite_Superior = round(limite_superior, 3),
Marca_Clase = round(marca_clase, 3),
Frecuencia_Absoluta = frecuencia_absoluta,
Frecuencia_Relativa = round(frecuencia_relativa, 4),
Frecuencia_Acumulada = frecuencia_acumulada,
fi_xi = round(fi_xi, 3),
fi_xi2 = round(fi_xi2, 3)
)
return(tabla)
}Una vez ya definida la función para construir la tabla de frecuencias (tarea que se realiza la cada vez que se abre el software y se desea cargar la función en el entorno de trabajo). Se procede a emplear la función para construir la tabla:
# Construir tabla de frecuencias
tabla_freq <- construir_tabla_frecuencias(longitud_petalo, parametros)
# Mostrar tabla
tabla_freq Clase Limite_Inferior Limite_Superior Marca_Clase Frecuencia_Absoluta
1 1 1.000 1.738 1.369 48
2 2 1.738 2.475 2.106 2
3 3 2.475 3.213 2.844 1
4 4 3.213 3.950 3.581 10
5 5 3.950 4.688 4.319 29
6 6 4.688 5.425 5.056 32
7 7 5.425 6.163 5.794 22
8 8 6.163 6.900 6.531 6
Frecuencia_Relativa Frecuencia_Acumulada fi_xi fi_xi2
1 0.3200 48 65.700 89.927
2 0.0133 50 4.213 8.873
3 0.0067 51 2.844 8.087
4 0.0667 61 35.812 128.254
5 0.1933 90 125.244 540.896
6 0.2133 122 161.800 818.101
7 0.1467 144 127.463 738.486
8 0.0400 150 39.188 255.943La tabla de frecuencias es la base para calcular las medidas de tendencia central y dispersión en datos agrupados. Cada fila representa un intervalo de clase y sus frecuencias asociadas. Si se desea exportar la tabla de frecuencias en un formato tabular para su presentación se utiliza la función write_xlsx como se muestra a continuación.
# Exportar la tabla de frecuencias
write_xlsx(tabla_freq, "tabla_frecuencias.xlsx")Al ejecutar esta linea de código R automáticamente guardará un archivo .xlsx en la carpeta del proyecto.
12.6 Medidas de Tendencia Central
Se define una función personalizada para calcular la media, mediana y moda a partir de la tabla de frecuencias.
# Función para calcular medidas de tendencia central
calcular_tendencia_central <- function(tabla, parametros) {
# Media aritmética
media <- sum(tabla$fi_xi) / parametros$n
# Mediana
n <- parametros$n
posicion_mediana <- n / 2
clase_mediana <- which(tabla$Frecuencia_Acumulada >= posicion_mediana)[1]
L <- tabla$Limite_Inferior[clase_mediana]
F_anterior <- ifelse(clase_mediana == 1,
0, tabla$Frecuencia_Acumulada[
clase_mediana - 1])
f_m <- tabla$Frecuencia_Absoluta[clase_mediana]
A <- tabla$Limite_Superior[clase_mediana] -
tabla$Limite_Inferior[clase_mediana]
mediana <- L + ((posicion_mediana - F_anterior) / f_m) * A
# Moda
clase_modal <- which.max(tabla$Frecuencia_Absoluta)
fa_ant <- ifelse(clase_modal == 1,
0, tabla$Frecuencia_Absoluta[
clase_modal - 1])
fa_sig <- ifelse(clase_modal == parametros$k,
0, tabla$Frecuencia_Absoluta[
clase_modal + 1])
d1 <- tabla$Frecuencia_Absoluta[clase_modal] - fa_ant
d2 <- tabla$Frecuencia_Absoluta[clase_modal] - fa_sig
if ((d1 + d2) == 0) {
moda <- NA
} else {
moda <- tabla$Limite_Inferior[clase_modal] + (d1 / (d1 + d2)) * A
}
return(list(media = media, mediana = mediana, moda = moda))
}En esta función la media se calcula como el promedio ponderado de las marcas de clase. La mediana y la moda se estiman usando fórmulas específicas para datos agrupados, considerando la posición dentro de la clase correspondiente, una vez ya definida la función se procede a utilizarla para calcular las medidas de tendencia central.
# Calcular medidas
tendencia <- calcular_tendencia_central(tabla_freq, parametros)
# Mostrar resultados
tendencia$media
[1] 3.748427
$mediana
[1] 4.306276
$moda
[1] 1.37685112.7 Medidas de Dispersión
Se utiliza una función personalizada para calcular el rango, la varianza, la desviación estándar y el coeficiente de variación.
# Función para calcular medidas de dispersión
calcular_dispersion <- function(tabla, parametros, media) {
# Rango aproximado
rango_aprox <- tabla$Limite_Superior[parametros$k] -
tabla$Limite_Inferior[1]
# Varianza
varianza <- (sum(tabla$fi_xi2) - (sum(tabla$fi_xi)^2 / parametros$n)) /
(parametros$n - 1)
# Desviación estándar
desviacion_std <- sqrt(varianza)
# Coeficiente de variación
cv <- (desviacion_std / media) * 100
return(list(
rango = rango_aprox,
varianza = varianza,
desviacion_std = desviacion_std,
cv = cv
))
}El rango es la diferencia entre el límite superior del último intervalo y el límite inferior del primero. La varianza y la desviación estándar se calculan usando las sumas ponderadas de las marcas de clase al cuadrado. El coeficiente de variación expresa la dispersión relativa respecto a la media. Para estos cálculos la función emplea las formulas presentadas en la sección anterior y una vez definida se procede al cálculo de las medidas de dispersión:
# Calcular medidas de dispersión
dispersion <- calcular_dispersion(tabla_freq, parametros, tendencia$media)
# Mostrar los resultados
dispersion$rango
[1] 5.9
$varianza
[1] 3.22793
$desviacion_std
[1] 1.796644
$cv
[1] 47.9306212.8 Medidas de Posición Relativa
Finalmente, se puede calcular cualquier cuartil o percentil usando una función personalizada.
# Función para calcular cuartiles y percentiles
calcular_posicion_relativa <- function(tabla,
parametros, posicion,
tipo = "cuartil") {
if (tipo == "cuartil") {
pos_valor <- posicion * parametros$n / 4
} else if (tipo == "percentil") {
pos_valor <- posicion * parametros$n / 100
}
clase_objetivo <- which(tabla$Frecuencia_Acumulada >= pos_valor)[1]
fa_anterior <- ifelse(clase_objetivo == 1, 0,
tabla$Frecuencia_Acumulada[clase_objetivo - 1])
valor <- tabla$Limite_Inferior[clase_objetivo] +
((pos_valor - fa_anterior) /
tabla$Frecuencia_Absoluta[clase_objetivo]) * parametros$amplitud
return(valor)
}Esta función permite calcular cualquier medida de posición relativa, como cuartiles o percentiles, utilizando la tabla de frecuencias y la fórmula correspondiente para datos agrupados. Una vez definida en el entorno de trabajo se procede a utilizar para calcular Q1 y P80 como en el ejemplo anterior:
# Calcular Q1
Q1 <- calcular_posicion_relativa(tabla_freq, parametros, 1, "cuartil")
Q1[1] 1.576172# Calcular P80
P80 <- calcular_posicion_relativa(tabla_freq, parametros, 80, "percentil")
P80[1] 5.37940612.9 Histograma
El histograma es un gráfico de barras que representa la distribución de frecuencias de los datos agrupados. Cada barra corresponde a un intervalo de clase, y su altura es proporcional a la frecuencia absoluta o relativa de ese intervalo.
Construcción en R:
hist(longitud_petalo,
breaks = seq(min(longitud_petalo),
max(longitud_petalo),
length.out = parametros$k + 1),
main = "Histograma de la Longitud del Pétalo",
xlab = "Longitud del Pétalo (cm)",
ylab = "Frecuencia",
col = "skyblue",
border = "black")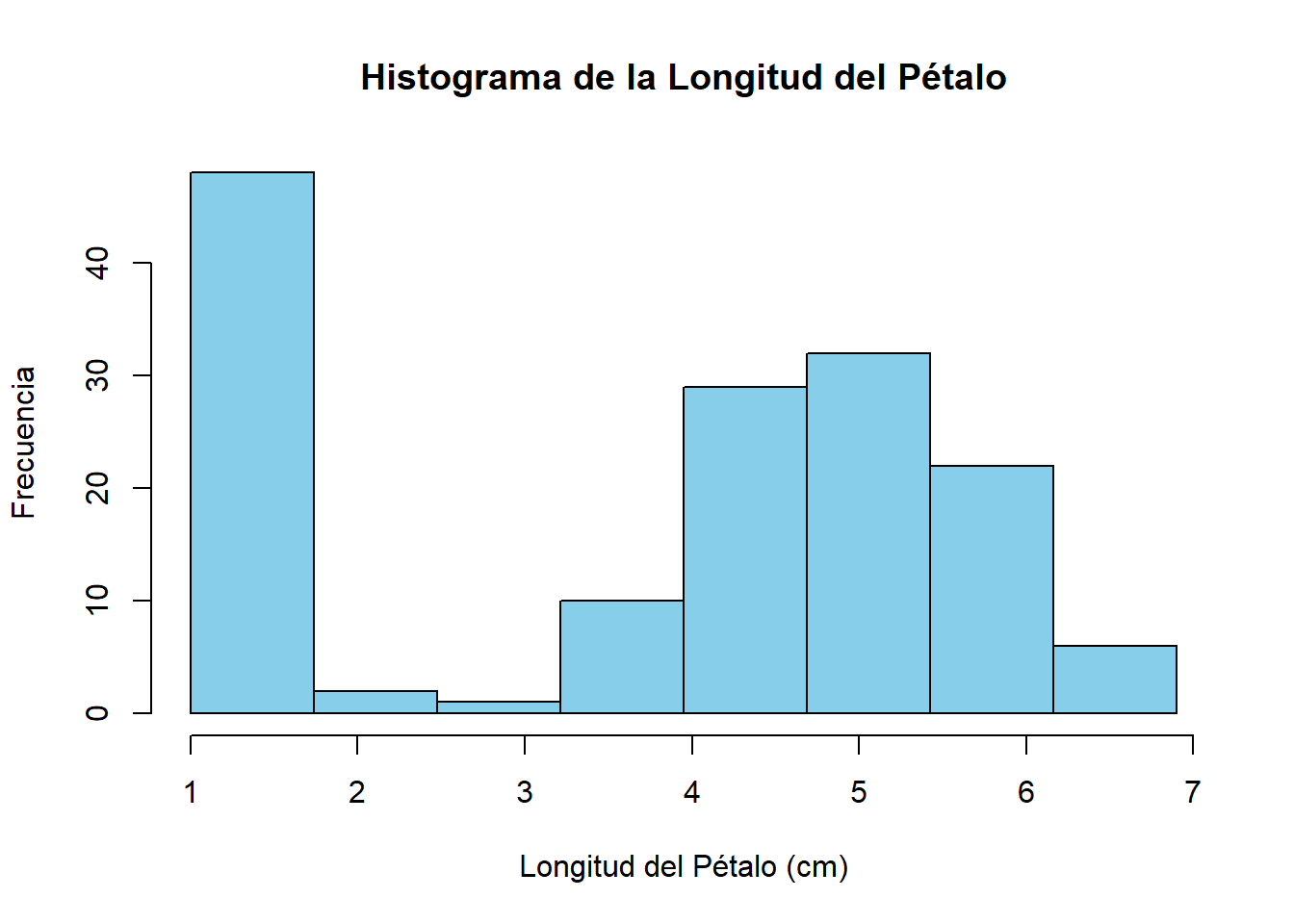
Explicación:
hist(): Función para crear histogramas en R.longitud_pedalo: Variable a graficar.breaks: Define los límites de los intervalos de clase. Se utilizaseq()para generar una secuencia de valores desde el mínimo hasta el máximo de la variable, dividida enk + 1puntos (dondekes el número de clases).main,xlab,ylab: Títulos y etiquetas de los ejes.col,border: Colores de las barras y del borde.
12.10 Polígono de Frecuencias
El polígono de frecuencias es un gráfico de líneas que conecta los puntos medios de las barras del histograma. Se construye uniendo los puntos correspondientes a las marcas de clase y sus respectivas frecuencias.
Construcción en R:
# Crear el polígono de frecuencias
plot(tabla_freq$Marca_Clase,
tabla_freq$Frecuencia_Absoluta,
type = "l", # "l" para líneas
main = "Polígono de Frecuencias de la Longitud del Pétalo",
xlab = "Longitud del Pétalo (cm)",
ylab = "Frecuencia",
col = "blue",
lwd = 2) # Grosor de la línea
# Agregar puntos en las marcas de clase
points(tabla_freq$Marca_Clase,
tabla_freq$Frecuencia_Absoluta,
col = "red", pch = 16) 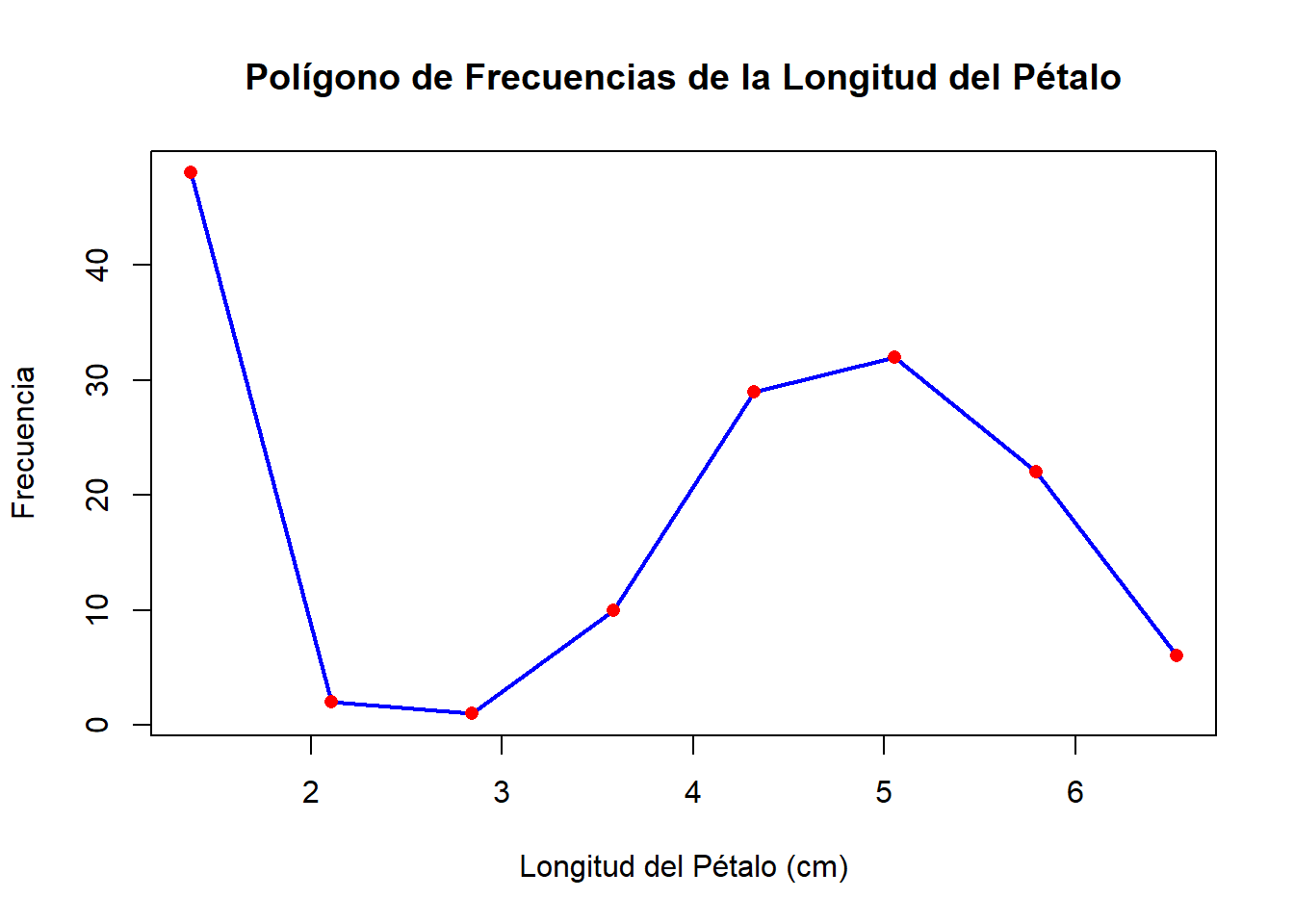
# pch = 16 para círculos rellenosExplicación:
plot(type = "l"): Crea un gráfico de líneas.tabla_freq$Marca_Claseytabla_freq$Frecuencia_Absoluta: Vectores con las marcas de clase y las frecuencias absolutas.points(): Agrega puntos en las marcas de clase para resaltar los valores.
12.11 Ojiva (Polígono de Frecuencias Acumuladas)
La ojiva es un gráfico de líneas que representa las frecuencias acumuladas. Se construye uniendo los puntos correspondientes a los límites superiores de los intervalos de clase y sus respectivas frecuencias acumuladas.
Construcción en R:
# Ojiva "Menor Que"
plot(tabla_freq$Limite_Superior, tabla_freq$Frecuencia_Acumulada,
type = "l",
main = "Ojiva 'Menor Que' de la Longitud del Pétalo",
xlab = "Longitud del Pétalo (cm)",
ylab = "Frecuencia Acumulada",
col = "blue")
# Ojiva "Mayor Que"
frecuencia_acumulada_mayor_que <- rev(cumsum(
rev(tabla_freq$Frecuencia_Absoluta)))
plot(tabla_freq$Limite_Inferior, frecuencia_acumulada_mayor_que,
type = "l",
main = "Ojiva 'Mayor Que' de la Longitud del Pétalo",
xlab = "Longitud del Pétalo (cm)",
ylab = "Frecuencia Acumulada",
col = "red")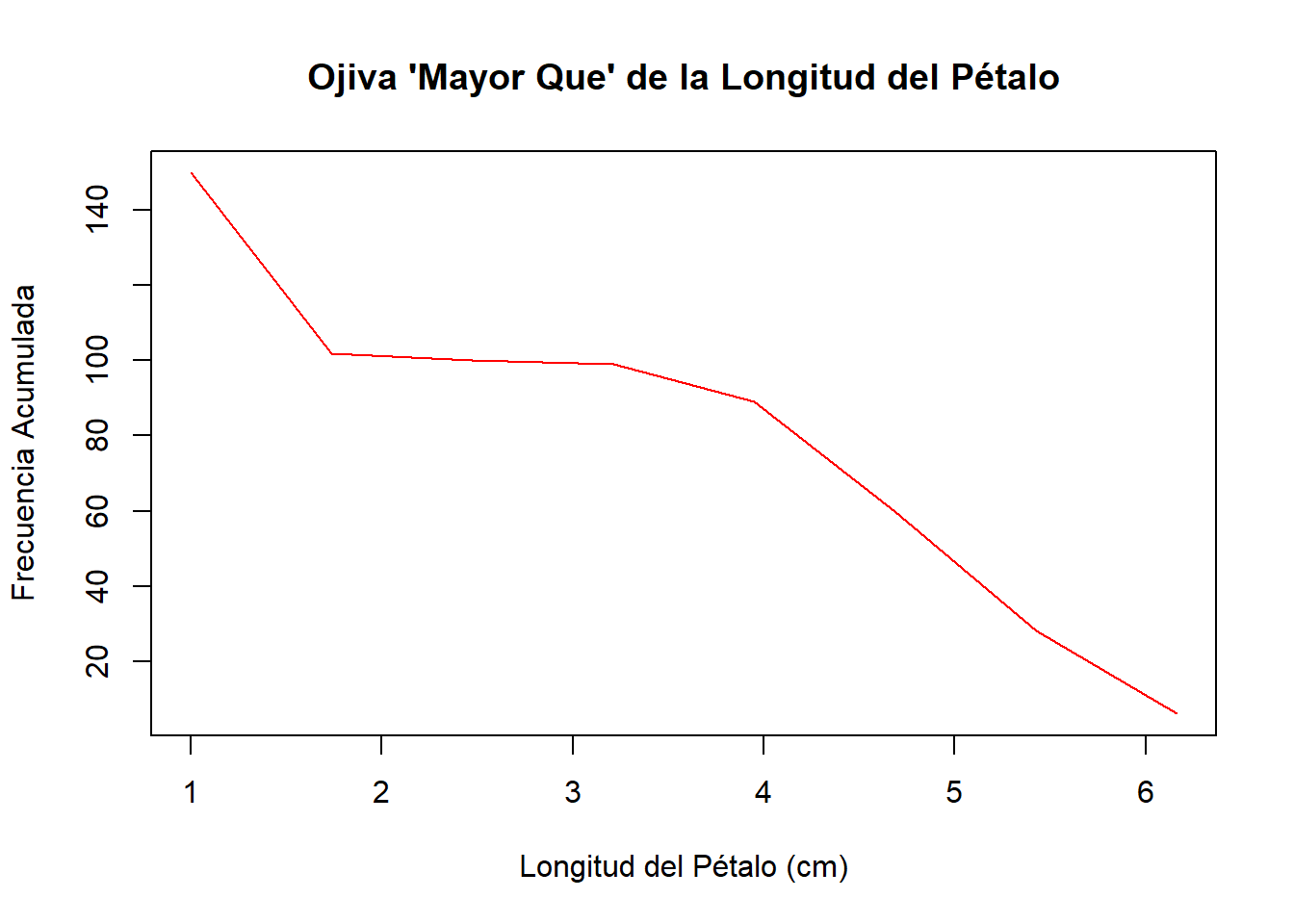
12.12 Gráfico de Barras
Aunque el histograma es el gráfico más común para datos agrupados, también se puede utilizar un gráfico de barras para representar las frecuencias de cada clase.
Construcción en R:
barplot(tabla_freq$Frecuencia_Absoluta,
names.arg = tabla_freq$Marca_Clase,
main = "Gráfico de Barras de la Longitud del Pétalo",
xlab = "Marca de Clase (cm)",
ylab = "Frecuencia Absoluta",
col = "orange",
border = "black")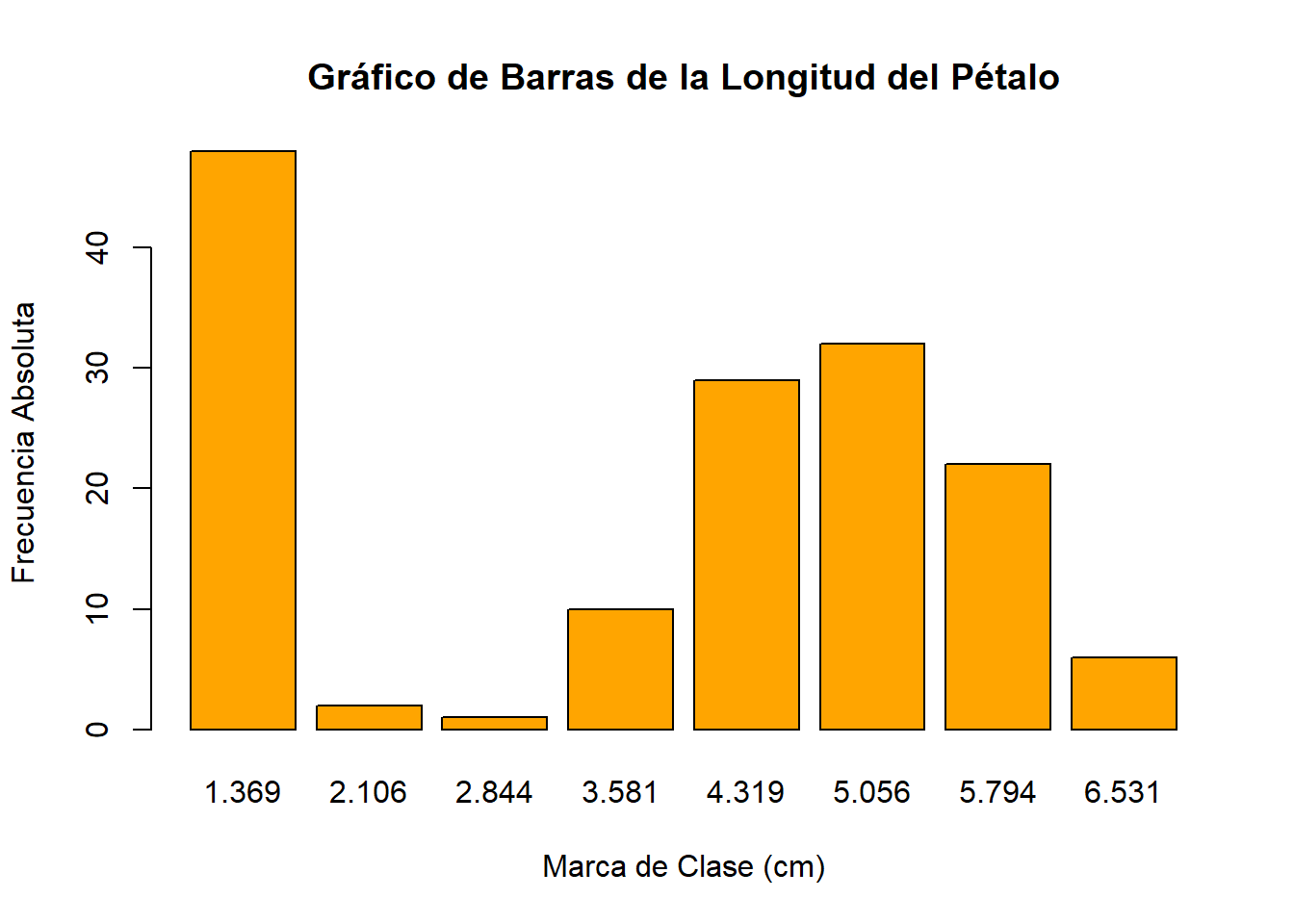
Explicación:
barplot(): Función para crear gráficos de barras en R.tabla_freq$Frecuencia_Absoluta: Vector con las frecuencias absolutas.names.arg: Etiquetas para cada barra (en este caso, las marcas de clase).
12.13 Cálculos a partir de una tabla de frecuencias
No siempre es posible encontrar la base de datos completa para poder construir la tabla de frecuencias y realizar las estimaciones, muchas veces se parte de una tabla de frecuencias debido a la sensibilidad de los datos, privacidad o porque los datos son muy antiguos y se han perdido los registos, para este ejemplo se va a explicar como usar las funciones partiendo de la tabla de frecuencias exportada a un archivo excel previamente en esta sección:
12.13.1 Importar la tabla de frecuencias
Cabe resaltar que para que esto funcione la tabla de frecuencias que se vaya a importar debe tener el mismo formato (numero y nombre de columnas ) que la tabla que se muestra a continuación:
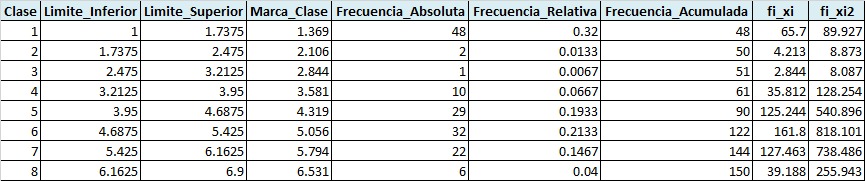
#Importar tabla de frecuencias
tabla<-read_excel("tabla_frecuencias.xlsx")12.13.2 Estimación de los parámetros de agrupación
Una vez importada la tabla de frecuencias adecuadamente se procede a estimar los parámetros de agrupación a partir de ella, ya que estos son indispensables para las funciones elaboradas para estimar las medidas de tendencia central, dispersión y posición relativa.
# Funcion personalizada para calcular los parametros
calcular_parametros_desde_tabla <- function(tabla) {
n <- sum(tabla$Frecuencia_Absoluta)
x_min <- min(tabla$Limite_Inferior)
x_max <- max(tabla$Limite_Superior)
rango <- x_max - x_min
k <- nrow(tabla)
amplitud <- (tabla$Limite_Superior[1] - tabla$Limite_Inferior[1])
return(list(
n = n,
x_min = x_min,
x_max = x_max,
rango = rango,
k = k,
amplitud = amplitud
))
}Una vez cargada la función al entorno de trabajo esta se utiliza con la tabla de frecuencias previamente importada para estimar los parámetros de agrupación
# Estimar los parametros de agrupacion a partir de la tabla de frecuencias
parametros_tabla <- calcular_parametros_desde_tabla(tabla)12.13.3 Estimación de los parámetros con las mismas funciones
Una vez ya se ha importado la tabla de frecuencias y estimado los parámetros de agrupación a partir de la tabla de frecuencias es posible usar las funciones previamente establecidas para calculas los parámetros como se muestra a continuación:
Medidas de tendencia central
# Calcular medidas tendencia_tabla <- calcular_tendencia_central(tabla, parametros_tabla) # Mostrar resultados tendencia_tabla$media [1] 3.748427 $mediana [1] 4.306034 $moda [1] 1.376596Medidas de dispersión
# Calcular medidas de dispersión dispersion_tabla <- calcular_dispersion(tabla, parametros_tabla, tendencia_tabla$media) # Mostrar los resultados dispersion_tabla$rango [1] 5.9 $varianza [1] 3.22793 $desviacion_std [1] 1.796644 $cv [1] 47.93062Medidas de posición relativa
# Calcular Q1 y P80 Q1_tabla <- calcular_posicion_relativa(tabla, parametros_tabla, 1, "cuartil");Q1_tabla[1] 1.576172P80_tabla <- calcular_posicion_relativa(tabla, parametros_tabla, 80, "percentil");P80_tabla[1] 5.378906
Como se puede observar siempre y cuando la tabla de frecuencias siga el formato propuesto las funciones seguirán operando con normalidad partiendo desde una base de datos completa o únicamente desde una tabla de frecuencias, cabe resaltar que el ajustar el formato de la tabla de frecuencias cuando se trabaja con una tabla de frecuencias y no con una base de datos completa es una tarea adicional que se debe llevar a cabo previo al análisis.
