19  Regresión Lineal Simple usando R

La regresión lineal simple es una técnica estadística fundamental para analizar la relación entre dos variables cuantitativas, permitiendo modelar y predecir el comportamiento de una variable dependiente a partir de una variable independiente. En el contexto de la agronomía, esta herramienta resulta esencial para comprender fenómenos como la relación entre el peso en cultivos o animales, entre otros ejemplos relevantes (Montgomery et al., 2021; López & González, 2018).

19.1 Fundamentos Teóricos

El modelo de regresión lineal simple se expresa mediante la siguiente ecuación:

\[\huge Y_i = \beta_0 + \beta_1 X_i + \varepsilon_i\]

En esta expresión:

  1. \(Y_i\) representa el valor observado de la variable dependiente para el individuo i.

  2. \(X_i\) es el valor observado de la variable independiente para el individuo i.

  3. \(\beta_0\) es el intercepto o constante, que indica el valor esperado de \(Y\) cuando \(X=0\).

  4. \(\beta_1\) es la pendiente, que representa el cambio promedio en \(Y\) por cada unidad de cambio en \(X\).

  5. \(\varepsilon_i\) es el término de error aleatorio, que recoge la variabilidad no explicada por el modelo.

El objetivo de la regresión es estimar los valores de \(\beta_0\)​ y \(\beta_1\)​ que mejor se ajustan a los datos observados. Para ello, se utiliza el método de mínimos cuadrados, que minimiza la suma de los cuadrados de las diferencias entre los valores observados y los valores predichos por el modelo (Montgomery et al., 2021).

Las fórmulas para los estimadores de mínimos cuadrados son:

\[\LARGE \hat{\beta_1} = \frac{\sum_{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y})}{\sum_{i=1}^{n} (x_i - \bar{x})^2}\]

\[\LARGE \hat{\beta_0} = \bar{y} - \hat{\beta_1}\bar{x}\]

donde \(\bar{x}\) y \(\bar{y}\) son las medias de las variables \(X\) y \(Y\) respectivamente.

19.2 Supuestos del Modelo

Para que los resultados de la regresión lineal simple sean válidos, es necesario que se cumplan los siguientes supuestos (López & González, 2018):

  1. Linealidad: La relación entre la variable independiente y la dependiente debe ser lineal. Esto significa que el efecto de \(X\) sobre \(Y\) es constante a lo largo de todo el rango de valores.

  2. Normalidad de los errores: Los residuos (diferencias entre los valores observados y los predichos) deben seguir una distribución normal.

  3. Homocedasticidad: La varianza de los errores debe ser constante para todos los valores de \(X\).

  4. Independencia: Las observaciones deben ser independientes entre sí, es decir, el valor de una observación no debe influir en el valor de otra.

El incumplimiento de estos supuestos puede llevar a conclusiones erróneas o a una interpretación incorrecta de los resultados.

19.3 Análisis Práctico en R

19.3.1 Instalación y carga de paquetes

El análisis inicia con la carga de los paquetes especializados y la exploración de los datos:

# Instalación y carga de paquetes necesarios
if (!require(tidyverse)) install.packages("tidyverse")
if (!require(car)) install.packages("car")
if (!require(lmtest)) install.packages("lmtest")
if (!require(nortest)) install.packages("nortest")

Se recomienda siempre inspeccionar los datos antes de analizarlos. En este ejemplo, se utiliza un conjunto de datos ficticio sobre el peso de padres e hijos empleado para explicar el análisis de correlación lineal:

# Datos del ejemplo: peso de padres (X) y peso de hijos (Y) en kilogramos
datos <- data.frame(
  Peso_Padres = c(78, 65, 86, 68, 83, 68, 75, 80, 82, 66),
  Peso_Hijos = c(60, 52, 68, 53, 65, 57, 58, 62, 65, 53)
)

Es recomendable graficar los datos para observar la posible relación lineal:

# Gráfico de dispersión
ggplot(datos, aes(x = Peso_Padres, y = Peso_Hijos)) +
  geom_point() +
  labs(title = "Relación entre el peso de padres e hijos",
       x = "Peso de padres (kg)",
       y = "Peso de hijos (kg)")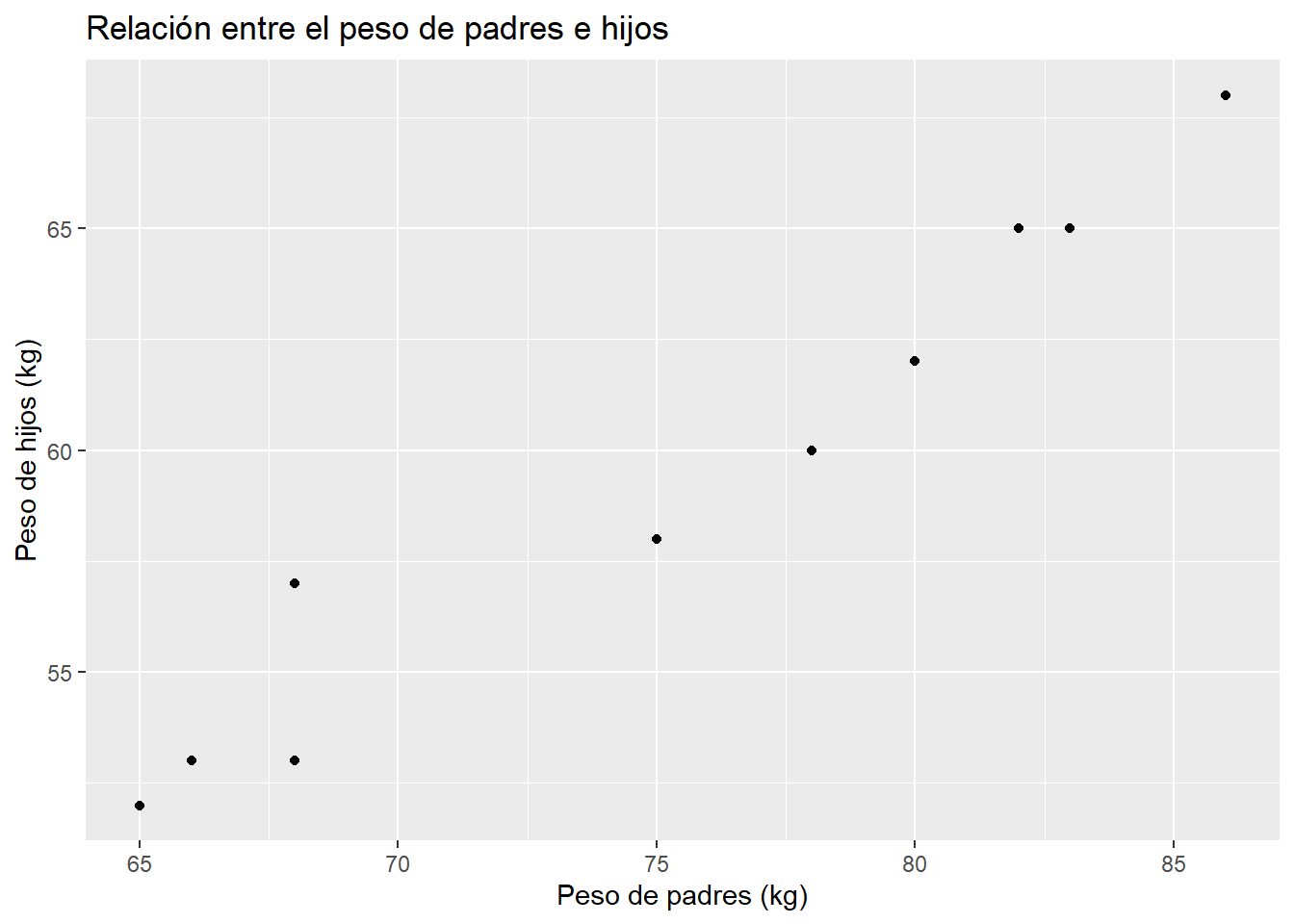

19.3.2 Ajuste del Modelo

Para ajustar el modelo, se utiliza la función lm(), cuya sintaxis general es:

modelo <- lm(Y ~ X, data = datos)

En este caso:

modelo <- lm(Peso_Hijos ~ Peso_Padres, data = datos)

Para obtener un resumen detallado del modelo, se emplea:

summary(modelo)

Call:
lm(formula = Peso_Hijos ~ Peso_Padres, data = datos)

Residuals:
     Min       1Q   Median       3Q      Max 
-1.35052 -1.11314 -0.02222  0.64948  2.72024 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  6.19857    4.37024   1.418    0.194    
Peso_Padres  0.70708    0.05791  12.209 1.88e-06 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.354 on 8 degrees of freedom
Multiple R-squared:  0.9491,    Adjusted R-squared:  0.9427 
F-statistic: 149.1 on 1 and 8 DF,  p-value: 1.879e-06

El resumen incluye los coeficientes estimados, sus errores estándar, valores t y p, así como el coeficiente de determinación (\(R^2\)), que indica la proporción de la variabilidad de \(Y\) explicada por \(X\).

19.3.3 Evaluación Crítica de Supuestos

19.3.3.1 Supuesto de Linealidad

Se evalúa mediante el gráfico de residuos vs valores ajustados. Si los residuos se distribuyen aleatoriamente alrededor de cero, el supuesto se considera cumplido.

plot(modelo, which = 1)  # Residuals vs Fitted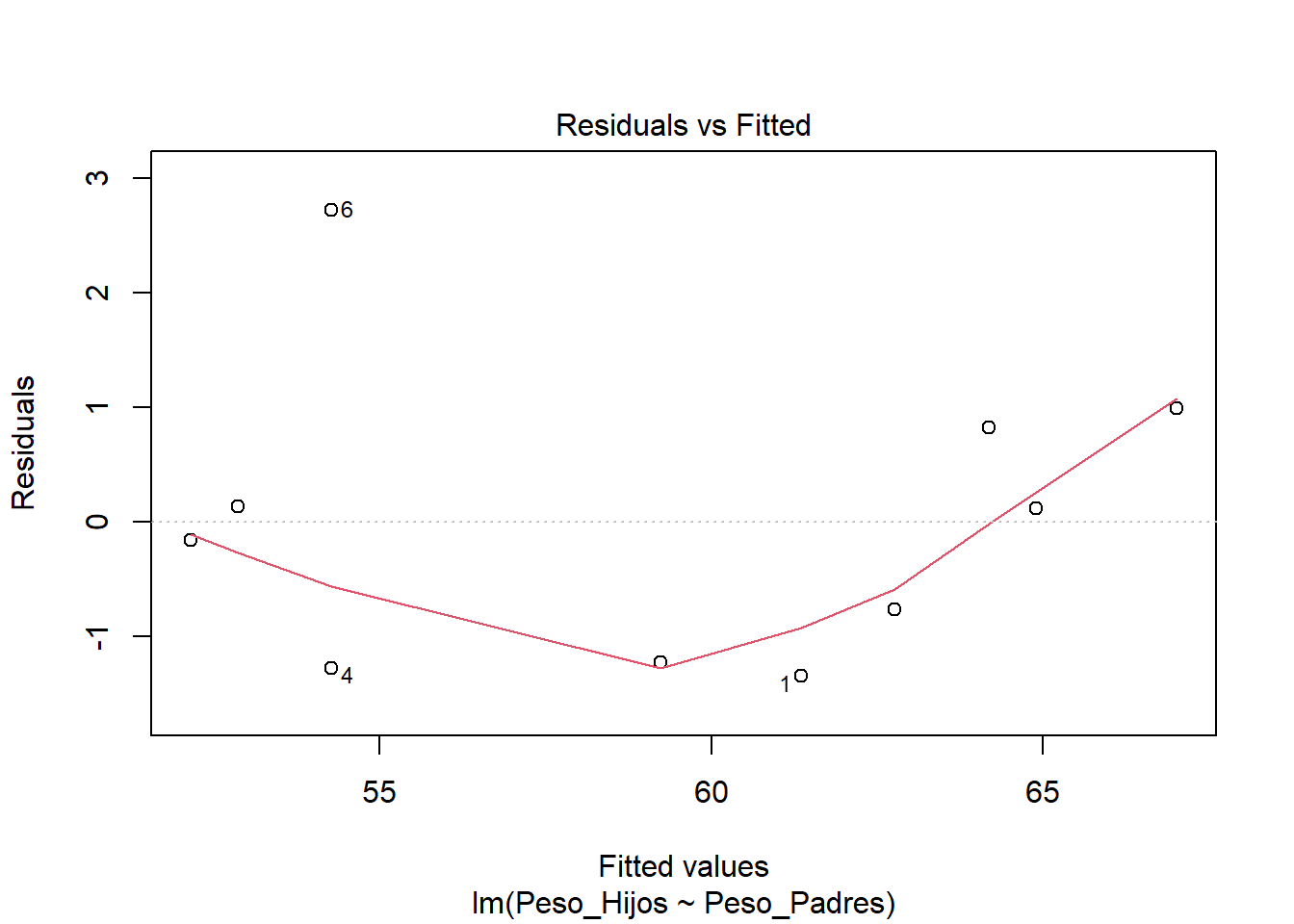

19.3.3.2 Supuesto de Normalidad

Se puede evaluar visualmente con un gráfico Q-Q y mediante pruebas estadísticas como Shapiro-Wilk y Anderson-Darling:

Gráfico Q-Q:

# Gráfico Q-Q
plot(modelo, which = 2)  # Normal Q-Q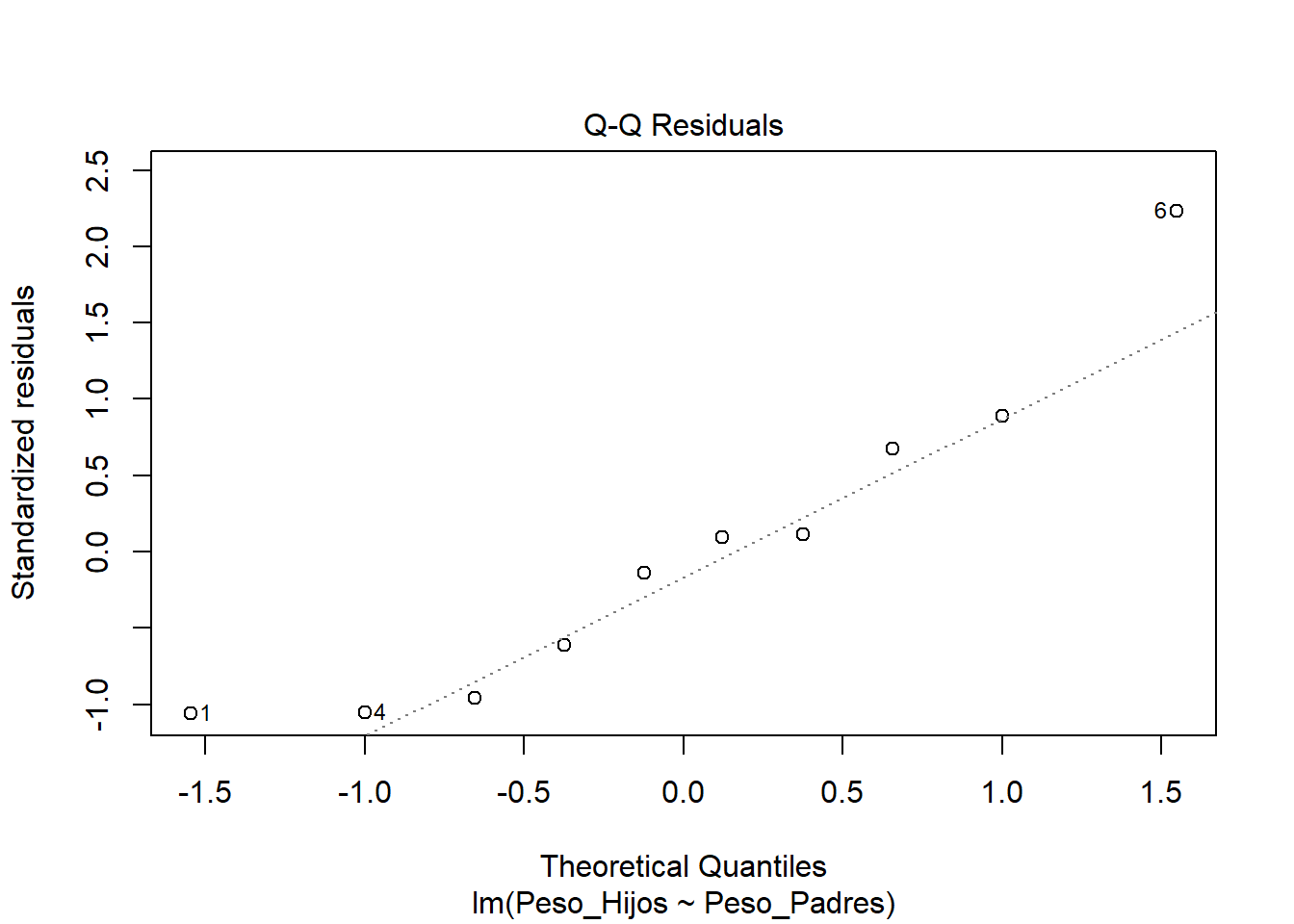

Prueba de Shapiro-Wilk:

  1. \(H_0​\): Los residuos siguen distribución normal

  2. \(H_a\)​: Los residuos no siguen distribución normal

shapiro.test(residuals(modelo))

    Shapiro-Wilk normality test

data:  residuals(modelo)
W = 0.9049, p-value = 0.2478

Prueba de Anderson-Darling (más potente para muestras grandes):

ad.test(residuals(modelo))

    Anderson-Darling normality test

data:  residuals(modelo)
A = 0.36544, p-value = 0.3604

19.3.3.3 Supuesto de Homocedasticidad

Se evalúa con la Prueba de Breusch-Pagan:

  1. \(H_0\)​: Varianza constante (homocedasticidad)

  2. \(H_a\)​: Varianza no constante (heterocedasticidad)

bptest(modelo)

    studentized Breusch-Pagan test

data:  modelo
BP = 0.71286, df = 1, p-value = 0.3985

19.3.3.4 Supuesto de independencia

En estudios experimentales, la independencia suele garantizarse mediante un diseño adecuado. En estudios observacionales, se recomienda analizar el contexto y, si es posible, realizar pruebas adicionales.

19.4 Predicción con el modelo ajustado

Una vez ajustado el modelo, se pueden realizar predicciones para nuevos valores de la variable independiente:

# Nuevos valores de Peso_Padres
nuevos_pesos <- data.frame(Peso_Padres = c(60, 75, 80))

# Predicción con intervalos de predicción
predicciones <- predict(modelo, nuevos_pesos, interval = "prediction")
predicciones
       fit      lwr      upr
1 48.62315 44.77666 52.46963
2 59.22929 55.95375 62.50484
3 62.76467 59.42443 66.10492

El resultado incluye el valor predicho y los límites inferior y superior del intervalo de predicción para cada nuevo valor.

19.5 Interpretación de Resultados

19.5.1 Coeficientes del Modelo

  1. Intercepto (\(\hat{\beta_0}\)​): Valor esperado de Y cuando X = 0

  2. Pendiente (\(\hat{\beta_1}\)​): Cambio promedio en Y por unidad de cambio en X

19.5.2 Bondad de Ajuste

El coeficiente de determinación (\(R^2\)) indica la proporción de variabilidad explicada:

\[\huge R^2 = \frac{SC_{Regresión}}{SC_{Total}}\]

​

  1. \(R^2 > 0.7\): Ajuste bueno

  2. \(-0.5 < R^2 < 0.7\): Ajuste moderado

  3. \(R^2 < 0.5\): Ajuste pobre

19.5.3 Significancia Estadística

La prueba F global evalúa:

  1. \(H_0\)​: \(\beta_1 = 0\) (no hay relación lineal)

  2. \(H_a\)​: \(\beta_1 \neq 0\) (existe relación lineal)

19.5.4 Criterios de Decisión para los supuestos

Supuesto Prueba Criterio de Aceptación
Normalidad Shapiro-Wilk p-valor > 0.05
Homocedasticidad Breusch-Pagan p-valor > 0.05
Linealidad Gráfico residuos Patrón aleatorio
Independencia Contexto experimental Diseño adecuado

19.5.5 Pasos para una Interpretación Integral y Conclusiones

  1. Evaluar significancia del modelo (prueba F global)

  2. Verificar supuestos mediante pruebas estadísticas y gráficos

  3. Interpretar coeficientes en el contexto del problema

  4. Evaluar bondad de ajuste (\(R^2\) y \(R^2\) ajustado)

  5. Identificar limitaciones del modelo

  6. Formular recomendaciones prácticas